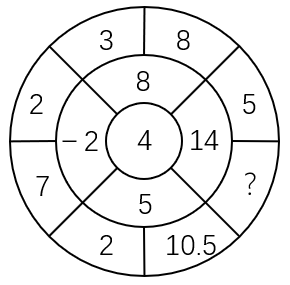
1·周末休息在家,爸爸要给小明出一道题,于是他在纸上画出了下方的图形,要小明仔细思考并寻找合适的规律后填上“?”处所空缺的数字,如果请你来帮助小明,那么“?”处的数字应该是多少?
A.2
B.6
C.3
D.4
2·箱子中装有4个不同的白球和6个不同的红球,若取出一个白球记2分,取出一个红球记1分,那么从袋子中取出5个球,总分不小于7分的取法有多少种?
A.180
B.186
C.196
D.206
3·某班级给不到100名的学生订牛奶和酸奶,其中6/7的学生订了牛奶,5/9的学生订了酸奶,还有一部分学生同时订了牛奶和酸奶,那么同时订了牛奶和酸奶的学生至少有多少名?
A.23
B.24
C.25
D.26
4·三名同事去买房,楼层有6层,其中两人决定要上下层挨着,另一人选择上下楼层都不挨着前两人,问三人最终选择楼层的方式有多少种可能?
A.12
B.24
C.35
D.48
1【答案】B
【解析】
第一步,本题考查趣味杂题。
![]()
第二步,观察图形可知,大圆整体被分成4份,且每个1/4的大圆均满足:大圆的两数相乘-中间圆的数字=中心圆数字的平方,即、、。

第三步,“?”处数字=。
因此,选择B选项。
2【答案】B
【解析】
第一步,本题考查排列组合问题。
![]()
第二步,任取5个球总分不小于7分的有3种不同的情况:取4个白球、1个红球共9分有=6(种);取3个白球、2个红球共8分有=60(种);取2个白球、3个红球共7分有=120(种),则共有6+60+120=186(种)。
因此,选择B选项。
3【答案】D
【解析】
第一步,本题考查容斥问题。
第二步,由总的学生数不足100且满足7和9的倍数,可知该班级共有学生63名,即54名学生订了牛奶,35名学生订了酸奶。
第三步,根据两集合容斥原理公式,列式54+35-同时订牛奶和酸奶的学生数=63-两个均没有订的学生数。要想两个都订的学生数尽可能少,即不存在两个均没有订的情况,则同时订牛奶和酸奶的学生数=54+35-63=26(名)(或可利用尾数法)。
因此,选择D选项。
4【答案】B
【解析】
第一步,本题考查排列组合问题。
![]()
第二步,其中两人选择(1、2)层或者(5、6)层时,另一人都有3种选择;当这两人选择(2、3),(3、4),(4、5)层时,另一人都有2种选择,则一共可能情况数为(3+3+2+2+2)×=24(种)。
因此,选择B选项。
