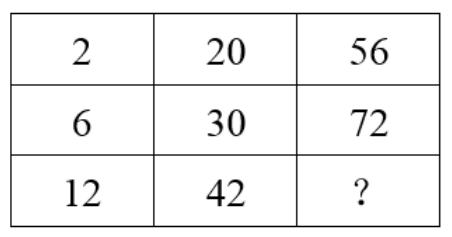
81. 请选择你认为最合理的一项,来填充所给数表的空缺项,使之符合原数表的排列规律:
A.80
B.81
C.90
D.89
【答案】C
【解析】
第一步,本题考查数图推理。
第二步,按列来看。第一列(12+2)-6×2=2,第二列(42+20)-30×2=2。规律为每一列的(第一项+第三项)-第二项×2=2。故第三列所求项为72×2+2-56=90。
因此,选择C选项。
82. 某单位辖有A、B、C三支施工队,分别编有员工388人、289人、339人。现将三支施工队整合为人数相等的甲、乙两支施工队,其中A队所有员工编入甲队,缺员部分按3:7的比例从B、C两队抽调,其余人员编入乙队。那么乙队中有( )人来自C队。
A.205
B.253
C.255
D.303
【答案】C
【解析】
第一步,本题考查基础计算问题。
第二步,根据题意,三支施工队总共388+289+339=1016人,则甲乙两支施工队各1016÷2=508,由于A队有388人,故甲队需从BC中共抽调508-388=120人。根据“3∶7的比例”可知从C抽调120×7/10=84人,故C队有339-84=255人被调入乙队。
因此,选择C选项。
83. 自然数12597能够分解为( )个质数之积。
A.2
B.3
C.4
D.5
【答案】C
【解析】
第一步,本题考查基础计算问题。
第二步,由于自然数12597=3×13×17×19,故能分解为4个质数之积。
因此,选择C选项。
84. 甲、乙、丙、丁四名干部因工作需要经常去团部开会,甲每隔5天去一次,乙每隔7天去一次,丙每隔9天去一次,丁每隔11天去一次。如果他们四人相遇过一次后,距离他们下次一起相遇需要等待的天数是( )天。
A.100
B.120
C.80
D.60
【答案】B
【解析】
第一步,本题考查约数倍数问题,用最小公倍数解题。
第二步,题目中出现每隔……每隔……每隔……,是最小公倍数解题的标志,每隔5天、每隔7天、每隔9天、每隔11天相当于每6天、每8天、每10天、每12天,因为6、8、10、12的最小公倍数为120,则下次一次相遇是120天后,即需要等待120天。
因此,选择B选项。
85. 小王在2016年2月1日在市图书馆借了一本书,共340页,前10天他的阅读速度为6页/天,第二个10天阅读速度为10页/天,由于图书借期为一月,他抓紧时间阅读,如果要在当月最后一天读完并归还图书,那么在剩下的时间内他的阅读速度应达到( )页/天。
A.15
B.20
C.18
D.24
【答案】B
【解析】
第一步,本题考查基础应用题。
第二步,由题意可得,剩下的页数为340-10×6-10×10=180页,剩下的时间为29-10-10=9天,因此在剩下的时间内他的阅读速度为180/9=20页/天。
因此,选择B选项。
