5. 一项工程,甲乙合作需要12天完成,乙丙需要20天完成,现由甲丙两队合作完成,其用时恰好是乙队单独完成时间的一半,问三队合作完成这项任务共需多少天?
A.8 B.9
C.10 D.11
6. 甲乙两车先后匀速从A、B两站出发,甲比乙先出发半小时,甲出发一小时后,两车距离为100千米,且此时甲距A站的距离是乙距B站的三倍,再过1小时,两车相遇,问甲车到B站时,乙车距离A站还有多远?
A.80 B.100
C.120 D.60
7. 某公司为员工定加班餐,前20人按原价20元/份,20人以上的部分按8折计,如果实际总价超过1200元,超过的部分,可以享受原价的6折。最终实际餐费一共花了1500元,问一共定了多少份加班餐?
A.105 B.100
C.85 D.95
8. 一个圆,取圆周上的六等分点连成一个矩形,则这个矩形的面积占圆总面积的比例为:
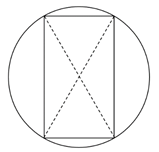

A.3:π B. :π

C. :π D.1:π
5.【答案】C
【解析】
第一步,本题考查工程问题。
第二步,赋值总工程量为12和20的最小公倍数60,则甲乙效率和为5,乙丙效率和为3。设乙的效率为x,则甲的效率为(5-x),丙的效率为(3-x)。
第三步,甲丙的效率和应为乙队的2倍,即(5-x)+(3-x)=2x,解得x=2,则甲的效率为3,丙的效率为1。三队合作效率为1+2+3=6。则总用时为60÷6=10(天)。
因此,选择C选项。
6.【答案】A
【解析】
第一步,本题考查行程问题。

第二步,甲出发一小时,乙出发了半小时,距离比为3∶1,时间比为1∶2,则速度比为3∶2。100千米的路程,两者经历1小时相遇,则每份速度为(千米/小时),则甲的速度为60千米/小时,乙的速度为40千米/小时。
第三步,A、B两站间总路程=1×60+100+0.5×40=180(千米),甲车经过180÷60=3(小时)后到B站,此时,乙只走了2.5小时,共走2.5×40=100(千米)。则乙车距离A站还有180-100=80(千米)。
因此,选择A选项。
7.【答案】D
【解析】
第一步,本题考查经济利润问题。
第二步,最终一共花了1500元,超过了1200元,超过了1500-1200=300(元),此时加班餐的单价为20×60%=12(元),则在这一部分的份数为300÷12=25(份)。
第三步,前20份按原价,总花费为20×20=400(元),打八折的部分总花费为1200-400=800(元),单价为20×80%=16(份),则这一部分的餐数为800÷16=50(份)。总共的数量为20+50+25=95(份)。
因此,选择D选项。
8.【答案】B
【解析】
第一步,本题考查几何问题。

第二步,如图,六等分点连成的矩形的宽为即为半径长度,矩形对角线为直径长度,设半径为1,则矩形的矩形对角线长度为2,根据勾股定理,矩形的长为。

第三步,圆的面积为πr²=π,矩形面积为,则面积比为︰π。
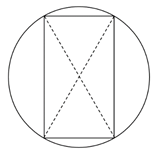
因此,选择B选项。
