1. 某部门10位老师旅游时参加竹筏漂流活动。每条竹筏最少乘坐3位老师,最多乘坐4位老师,竹筏之间无区别。那么10位老师乘坐竹筏的组合方式有:
A.540种 B.1200种
C.4200种 D.8400种
2. 有三杯溶质相同的某种盐溶液A、B、C,溶液浓度分别为30%、25%、28%。那么如果想要在三杯溶液中各取一些混合得到浓度为27%的溶液,以下取出溶液质量比例不可能实现目的的是:
A.1︰2︰1 B.2︰5︰4
C.3︰7︰5 D.4︰8︰7
3. 小华想通过掷飞镖的形式决定周末是学习还是玩耍。于是他在等边三角形纸板ABC的底边BC上任取一点P,然后连接顶点A与P得到△ABP和△ACP,如果飞镖掷进△ABP就学习,掷进△ACP就玩耍。如果小华想提前预设学习的概率是玩耍概率的2/3,那么BP的长度是△ABC边长的:
A.1/3 B.2/5
C.3/7 D.4/9
4. 在一次名师风采大赛中,参赛的25位老师得到的最终分数均为正整数且均不相同,所有人平均分数为84分,那么分数低于70分的老师最多有多少人?
A.10人 B.9人
C.8人 D.7人
1.【答案】D
【解析】
第一步,本题考查排列组合问题。
![]()
第二步,10位老师分三组数字组合只有(3,3,4)一种。因此可以考虑先挑出1位老师有=10(种),然后将剩余的9位老师平均分成3组有=280(种),再将挑出的那位老师随机放入3组中的某组有3种放法。总的组合方式为10×280×3=8400(种)。
因此,选择D选项。
2.【答案】D
【解析】
第一步,本题考查溶液问题。
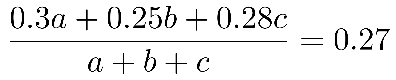
第二步,假设三杯溶液取出的质量分别为a、b、c,由题意有。化简有3a+c=2b。
第三步,代入四个选项,只有D选项不满足3a+c=2b。
因此,选择D选项。
3.【答案】B
【解析】
第一步,本题考查几何问题与概率问题的杂糅。
第二步,在几何概率中,部分面积与整体面积之比即为概率,因此学习概率是玩耍概率的2/3即△ABP和△ACP面积之比为2︰3。
第三步,如图所示,容易发现△ABP和△ACP是两个同高的三角形,因此面积之比为底边之比,即2︰3。那么BP︰BC=2︰5。

因此,选择B选项。
4.【答案】D
【解析】
第一步,本题考查最值问题。
第二步,每个人分数均不相同且为正整数,总分数是84×25=2100。由于本题不是典型的数列构造,正向入手较难,因此可采取代入排除。
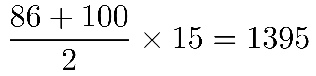
第三步,问最多,从A开始代入。假如低于70分的有10人,不低于70分的15人最多可得到100到86的分数,和为(分);此时低于70分的考生最多是69、68、67、……60,总得分为,两者加和为2040分,达不到2100分,排除。
代入B选项,同理高分16人最多得分为1395+85,低分9个人总分最多645-60,总分加和为2040+(85-60)=2065,达不到2100分,排除;而C选项同理总分加和应为2065+(84-61)=2088,仍达不到2100分,排除。验证D选项总分为2088+(83-62)=2109,超过2100分,符合题意。
因此,选择D选项。
